

Finally, the instructor can illustrate how different sample sizes influence the normality of the distribution by repeating the exercise with samples of 5 and 10.For each situation, the instructor should point out that regardless of the shape of the parent population, the sampling distribution should be approximately normal. A drop-down menu allows the choice of skewed right, uniform and normal distributions. The instructor can repeat the sampling process with different shapes of parent populations.The instructor should point out that even though the parent population is skewed to the left, the distribution of the mean coin dates is approximately normal.
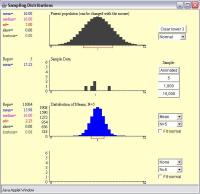
The instructor can use the "1000" button to take a large number of samples and allow the students to watch the sampling distribution build into an approximately normal distribution.The instructor can point out that this histogram is crude, due to the small number of samples from which it is constructed. The instructor will continue to take samples one at a time until the same number have been taken as were in the histogram assembled by hand.The instructor should point out both the values of the individuals in the second graph and the mean of the sample that appears in blue on the third graph. Point out that these would be equivalent to each sample of coins the class put together. The instructor should take samples of n=25 from this distribution one at a time.The instructor should then open the applet and construct a left skewed distribution resembling the distribution of the individual coin dates.The applet can serve as a method to more quickly take samples from the population. This serves as a lead into using the applet. The instructor should also point out that there are too few means to clearly see the distribution. the distribution of means is more symmetric than the distribution of the individual coin dates.For example, some students may have coins that date back to the 1940s, but the averages will typically be between 19. the distribution is more compact than the original distribution.the distribution is made up of the means of different samples from the population of interest.When this histogram is complete, the instructor should point out that.The instructor should then mark these on a dotplot or histogram on the board or an overhead. This is done by calling on each group (or individual student) to give their sample mean. The instructor "assembles" a dot plot or histogram of the sample means created by each student or group.The students then calculate the average of 30 coins to create their own sample statistic.This idea will form the basis for illustrating the Central Limit Theorem in later steps. If not, an instructor may need to guide them to this point. Based on the description in the handout, most students will get this idea. This distribution should be skewed to the left. coins and describe what they believe it will be. Students are asked to think about the distribution of the dates on U.S.By having the students assemble a sampling distribution, they can more readily understand that a sampling distribution is made up of a collection of sample statistics from different samples. In this activity students are exposed to the concept of sampling distributions by creating a sampling distribution as a class.


 0 kommentar(er)
0 kommentar(er)
